[문제]
Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner.

How many such routes are there through a 20×20 grid?
[풀이]
intGrid = 20
listFirst = [1 for i in range(0,intGrid+1)]
#listFirst = []
#for i in range(0,intGrid+1):
# listFirst.append(1)
for y in range(0,intGrid):
listSecond = []
[listSecond.append(1) if x==0 else listSecond.append(listSecond[x-1]+listFirst[x]) for x in range(0, intGrid+1)]
# for x in range(0,intGrid+1):
# if x==0:
# listSecond.append(1)
# else:
# listSecond.append(listSecond[x-1]+listFirst[x])
listFirst = listSecond
print(listSecond[-1])
'''
이 문제를 푸는 방법을 알고 있어서 쉽게 풀었다
경로의 수 구하기는 간단하다

시작점을 제외한 선이 만나는 모든 부분에 최단 경로의 수를 적어주면 된다.
각 사이드(시작점과 꺾이지 않은 직선으로 연결된 사이드)는 최단 거리로 갈 수 있는 방법이 모두 1가지 뿐이다.


사이드에 1을 모두 써줬으면 좌측 상단부터 수를 채워넣는다.
비어있는 부분은 (왼쪽 경우의 수 + 위쪽 경우의 수)를 하면 된다.
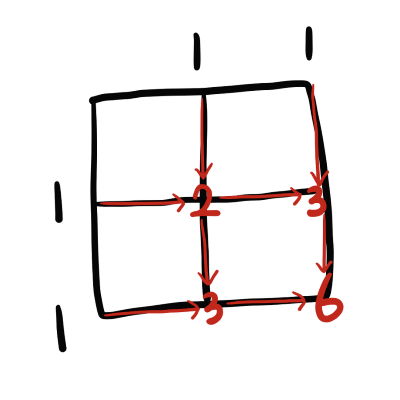
위의 과정대로 하면 2x2 그리드의 최단 경로의 수는 6이다.
이 과정 그대로 문제를 풀었다.
문제를 풀기위해서 필요한건 바로 윗줄과 현재 줄 두개니까 리스트 2개를 만들었다.
제일 첫 번째 리스트는 전부 1이니까 list comprehension을 사용해서 1만 들어간 리스트를 만들었다.
그리고 두번째 리스트의 0번인덱스는 1로 고정하고,
다음 인덱스부터는 두번째리스트[인덱스-1] + 첫번째리스트[인덱스]로 값을 넣었다.
두번째 리스트의 값이 모두 채워지면 두번째 리스트의 값을 첫번째 리스트에 넣어주고
다음 리스트를 만들기 위해 두번째 리스트를 초기화 했다.
회색으로 주석처리한 부분이 첫 풀이고 주석 바로 윗 줄이 list comprehension으로 푼 풀이다.
이번 문제에선 list comprehension에 if문을 사용해봤다!
'''
'파이썬' 카테고리의 다른 글
| [Project Euler]17. Number letter counts (0) | 2021.06.10 |
|---|---|
| [Project Euler]16. Power digit sum (0) | 2021.06.10 |
| [Project Euler]14. Longest Collatz sequence (0) | 2021.06.09 |
| [Project Euler]13. Large sum (0) | 2021.06.07 |
| [Project Euler]12. Highly divisible triangular number (0) | 2021.06.06 |